6 Test of outliers
In statistics, an outlier is a data point that differs significantly from other observations. An outlier may be due to variability in the measurement or it may indicate experimental error; the outlers are sometimes excluded from the data set. An outlier can cause serious problems in statistical analyses.
There are two types of outliers;
1. Univariate outliers (Z-Score)
2. Multivariate outliers (Mahalanobis Distance)
A univariate outlier is a data point that consists of an extreme value on one variable. A multivariate outlier is a combination of unusual scores on at least two variables. Both types of outliers can influence the outcome of statistical analyses.
6.1 Test of Univariate outliers
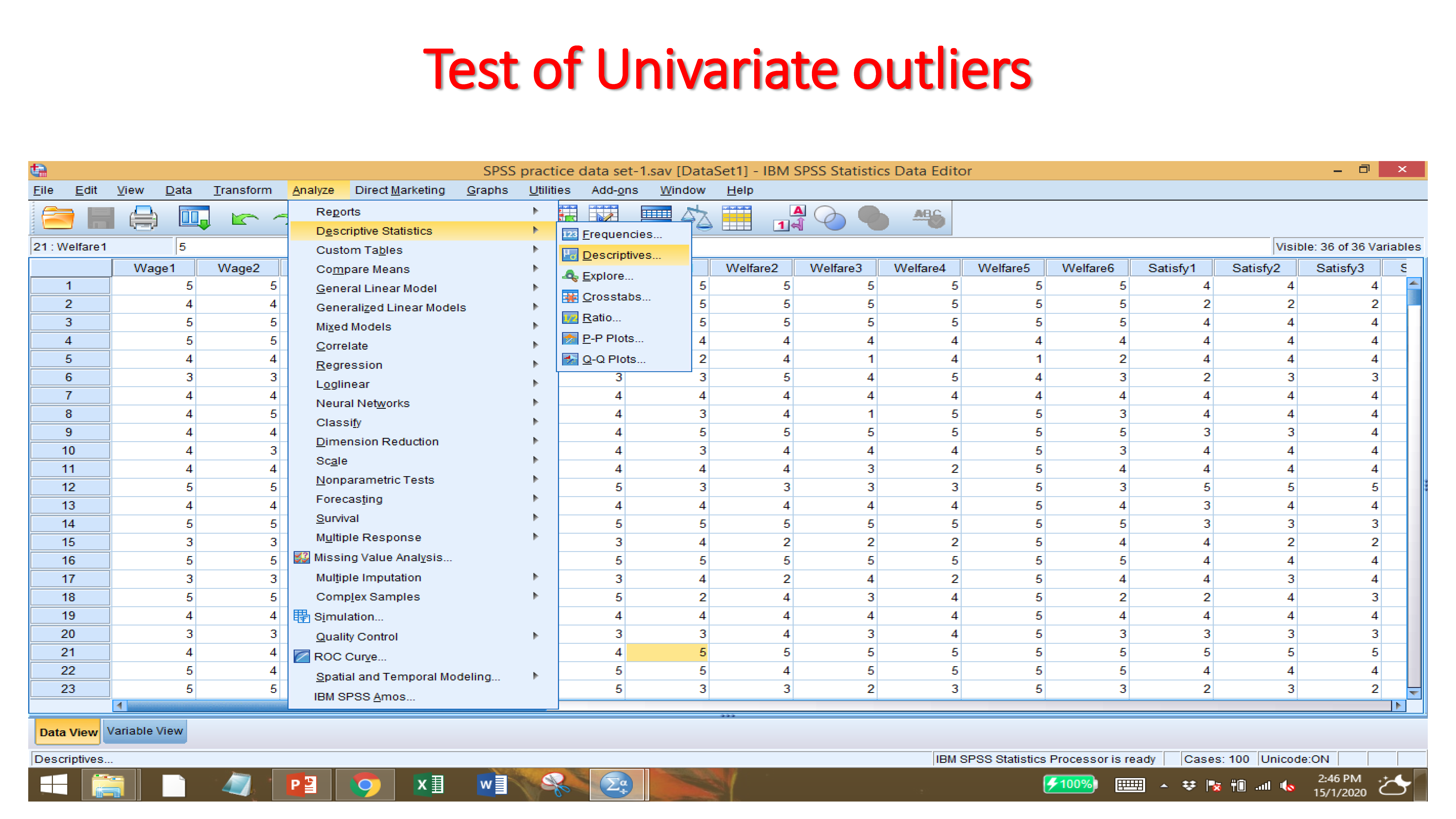
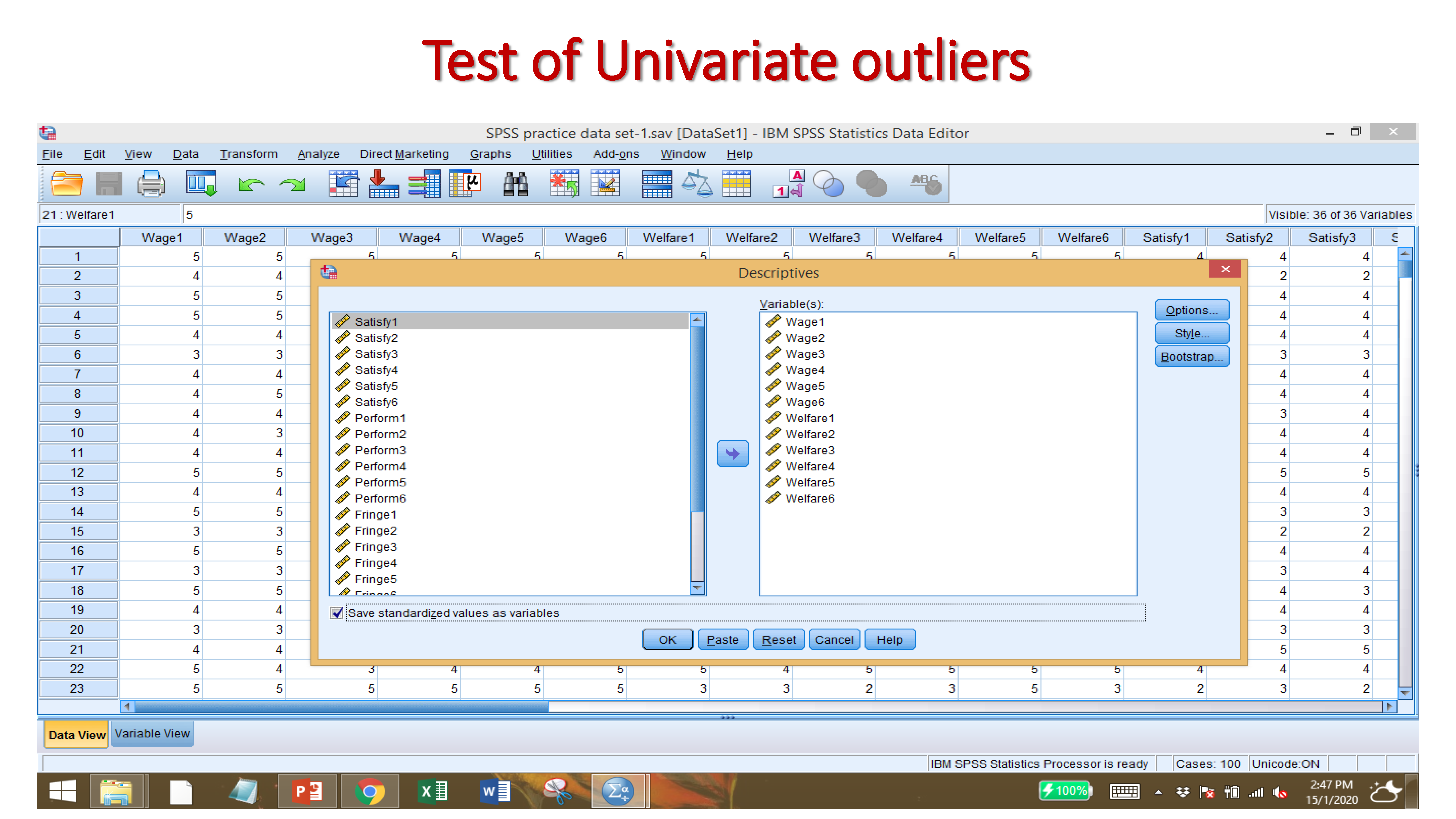
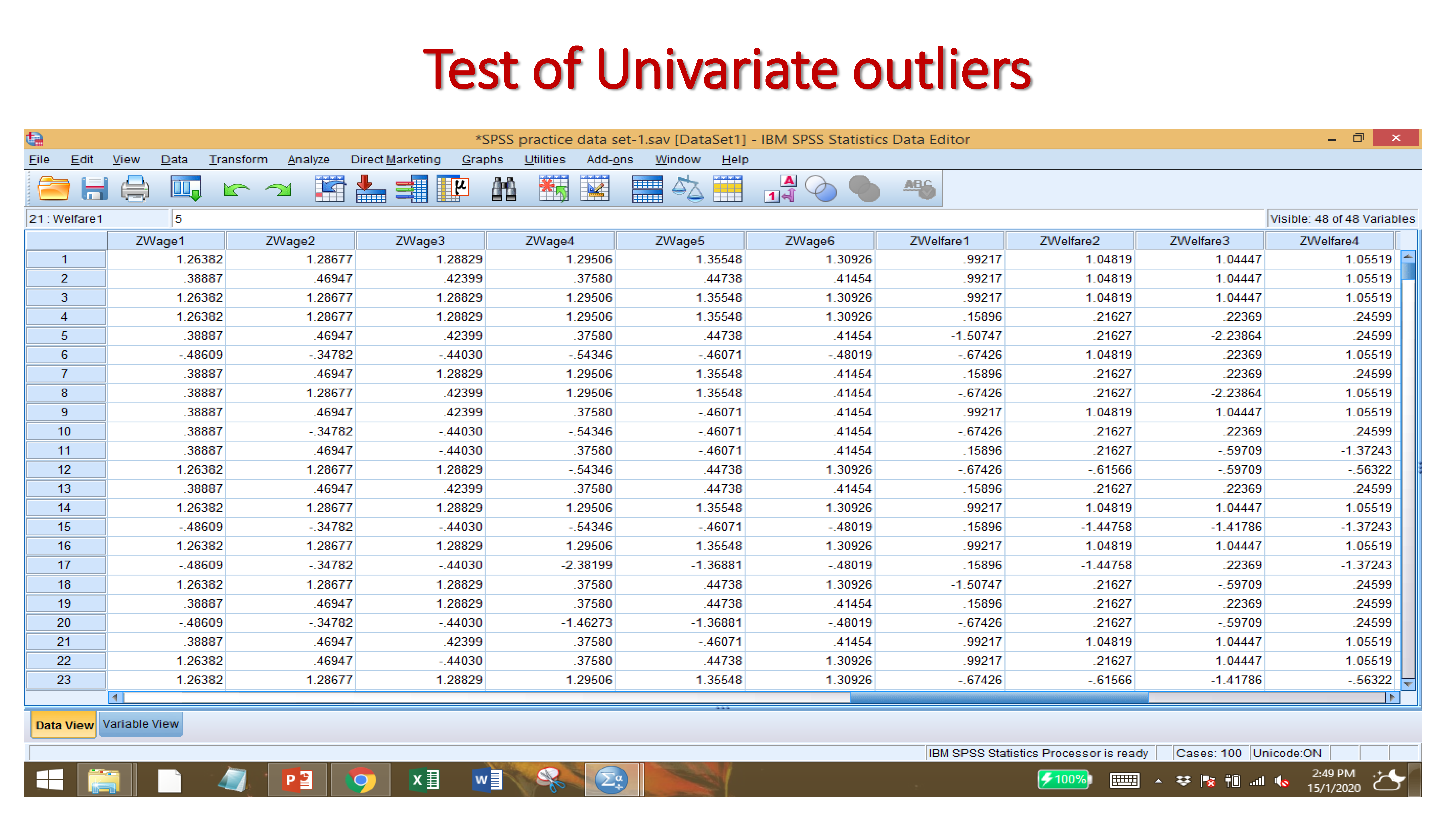
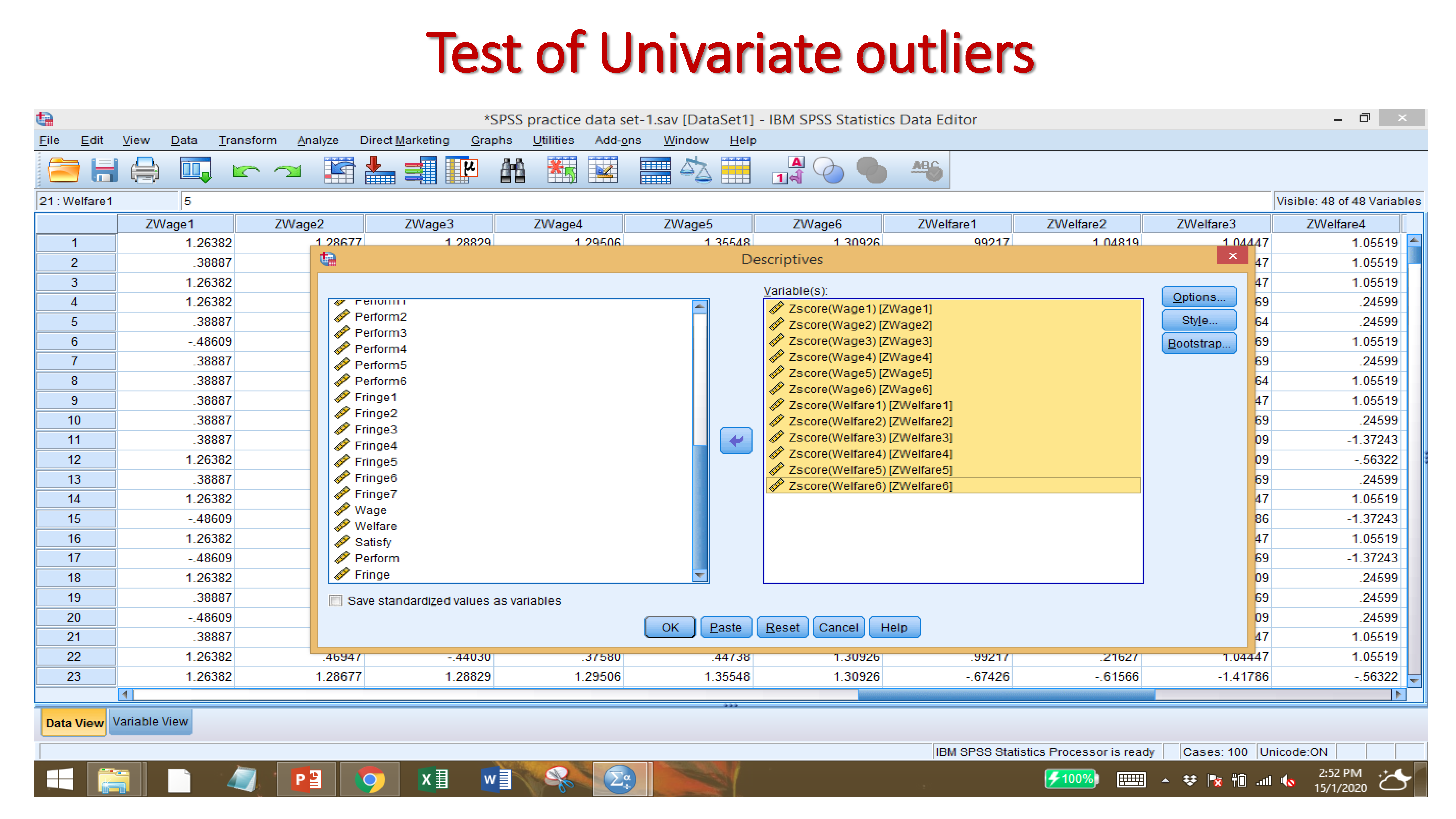

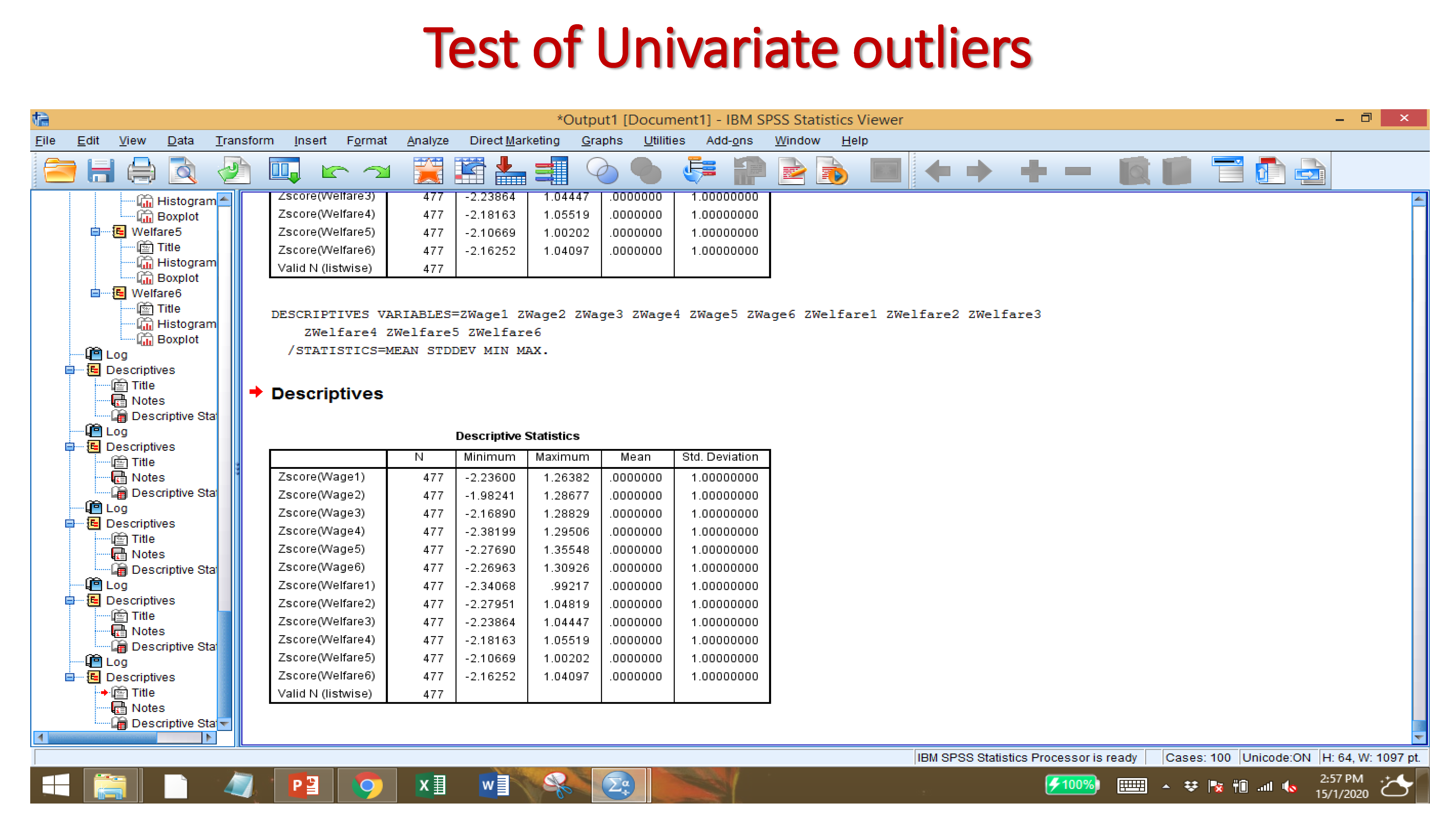
If the Z-Score Value beyond the value +3.29 to -3.29 for a large sample size (more than 80) then there is outliers. If the Z-Score Value beyond the value +2.50 to -2.50 for the case of small sample size (less than 80 samples) then there is outliers.
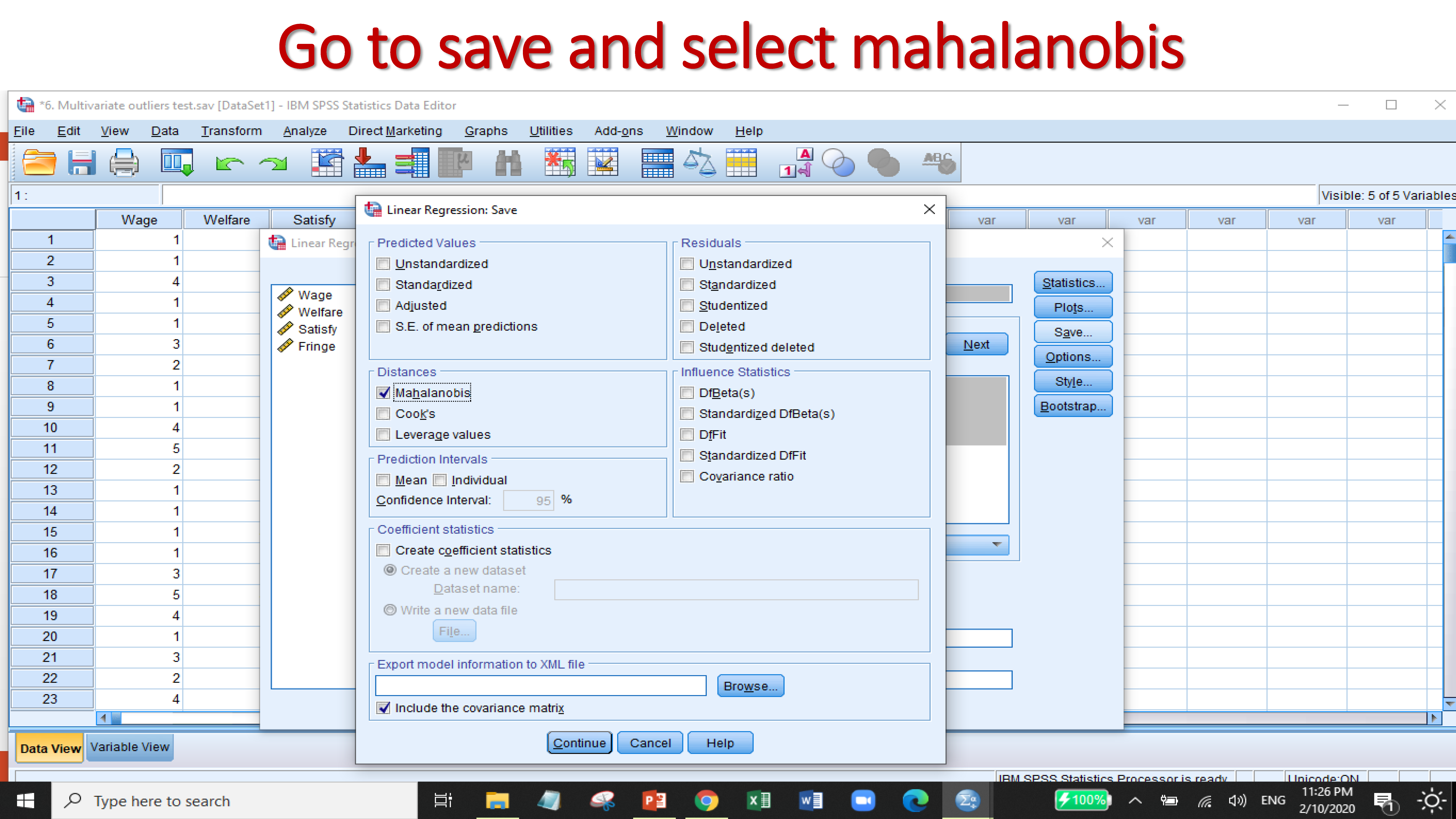
6.2 Test of multivariate outliers
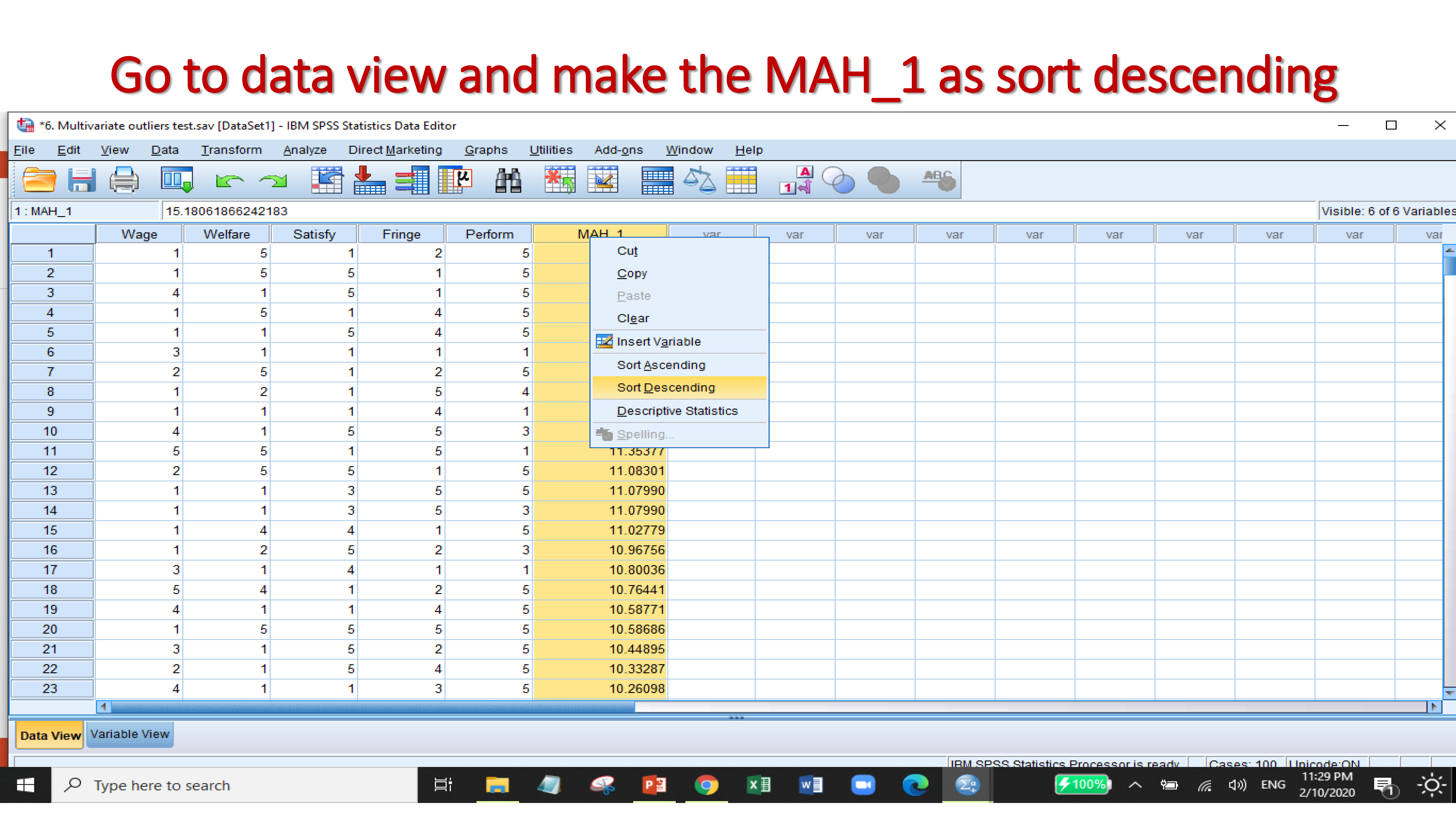
A multivariate outlier is a combination of unusual scores on at least two variables. Both types of outliers can influence the outcome of statistical analyses. The multivariate outliers can be identified by the test of
- Mahalanobis Distance
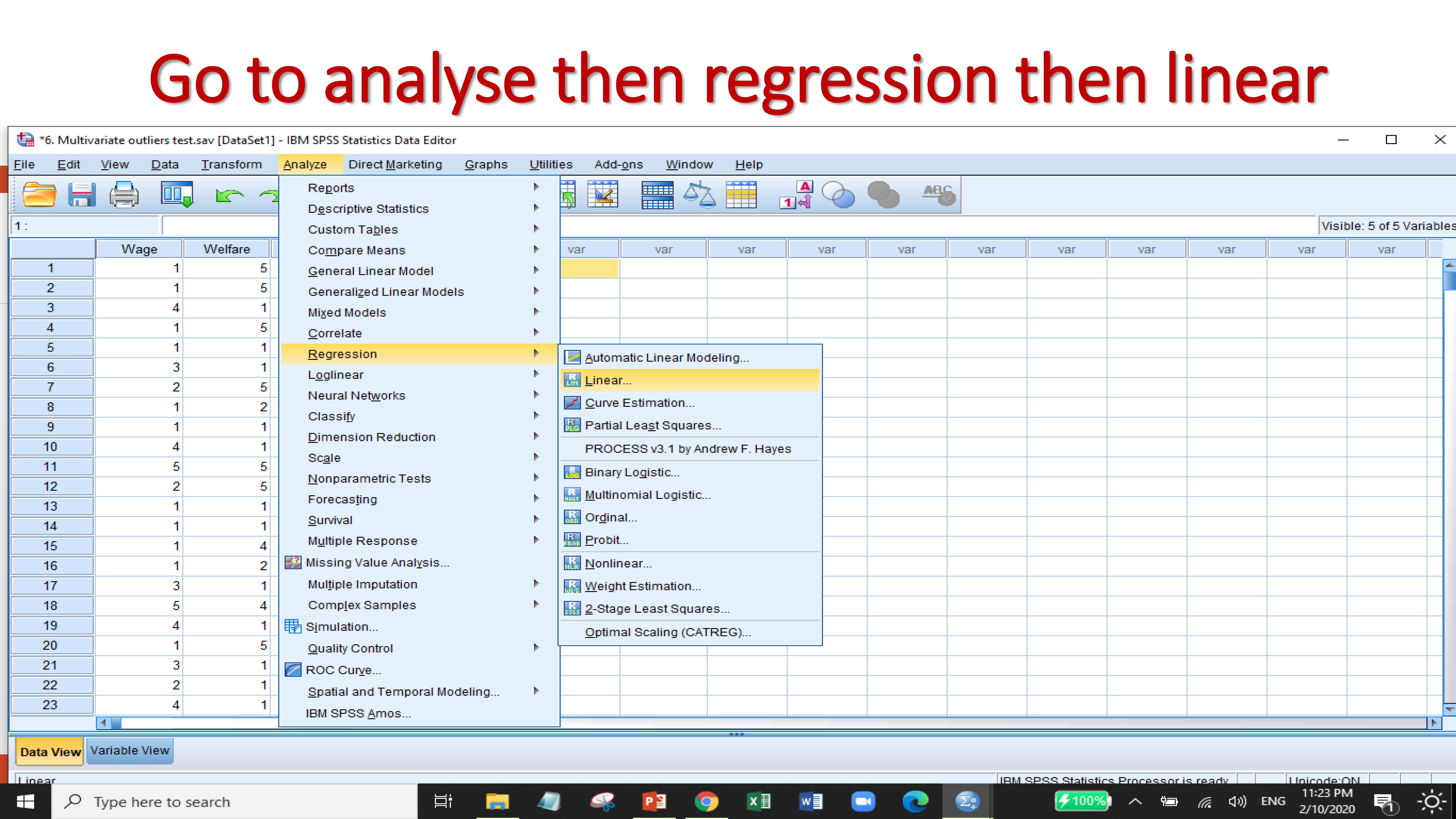
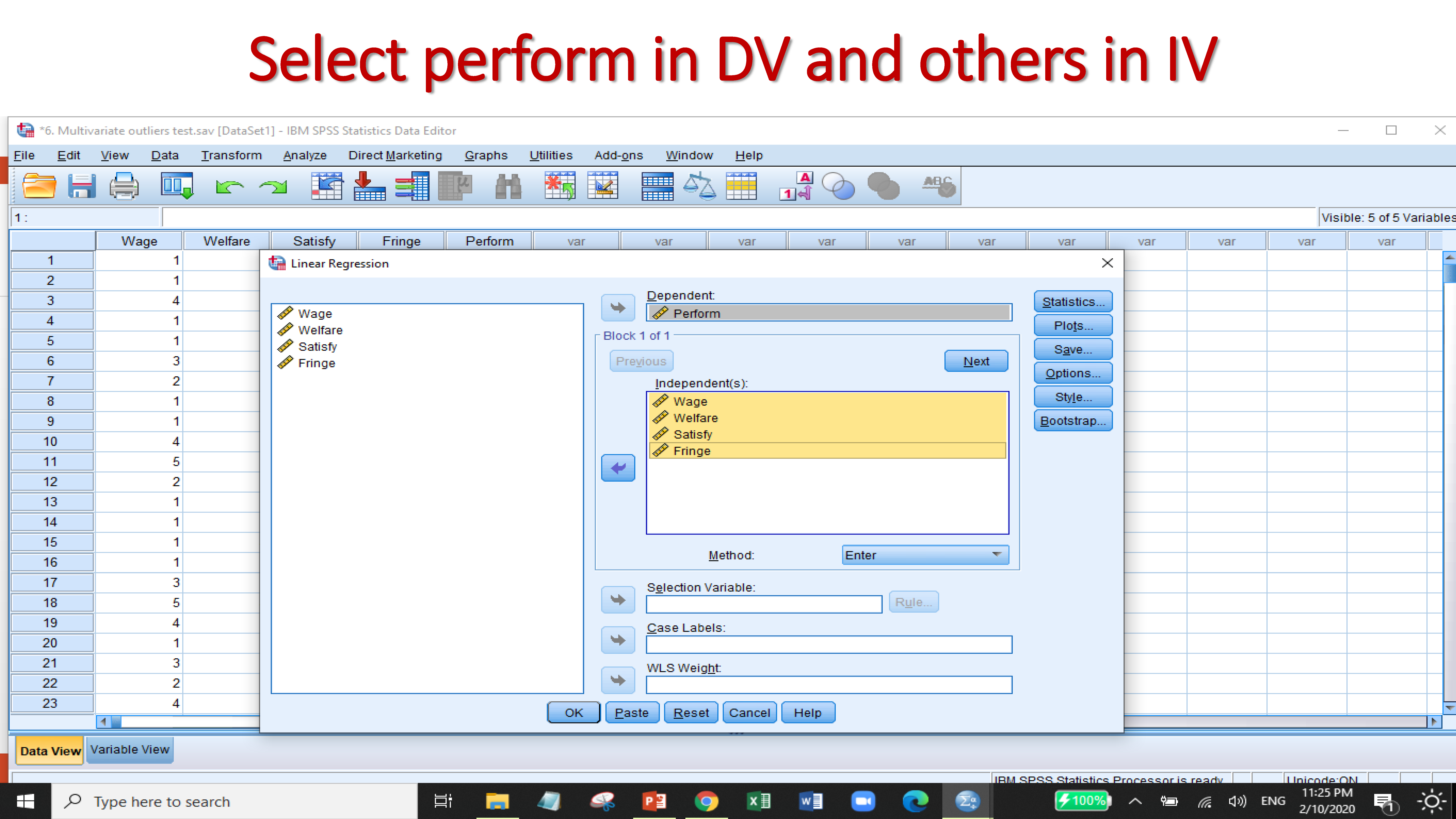

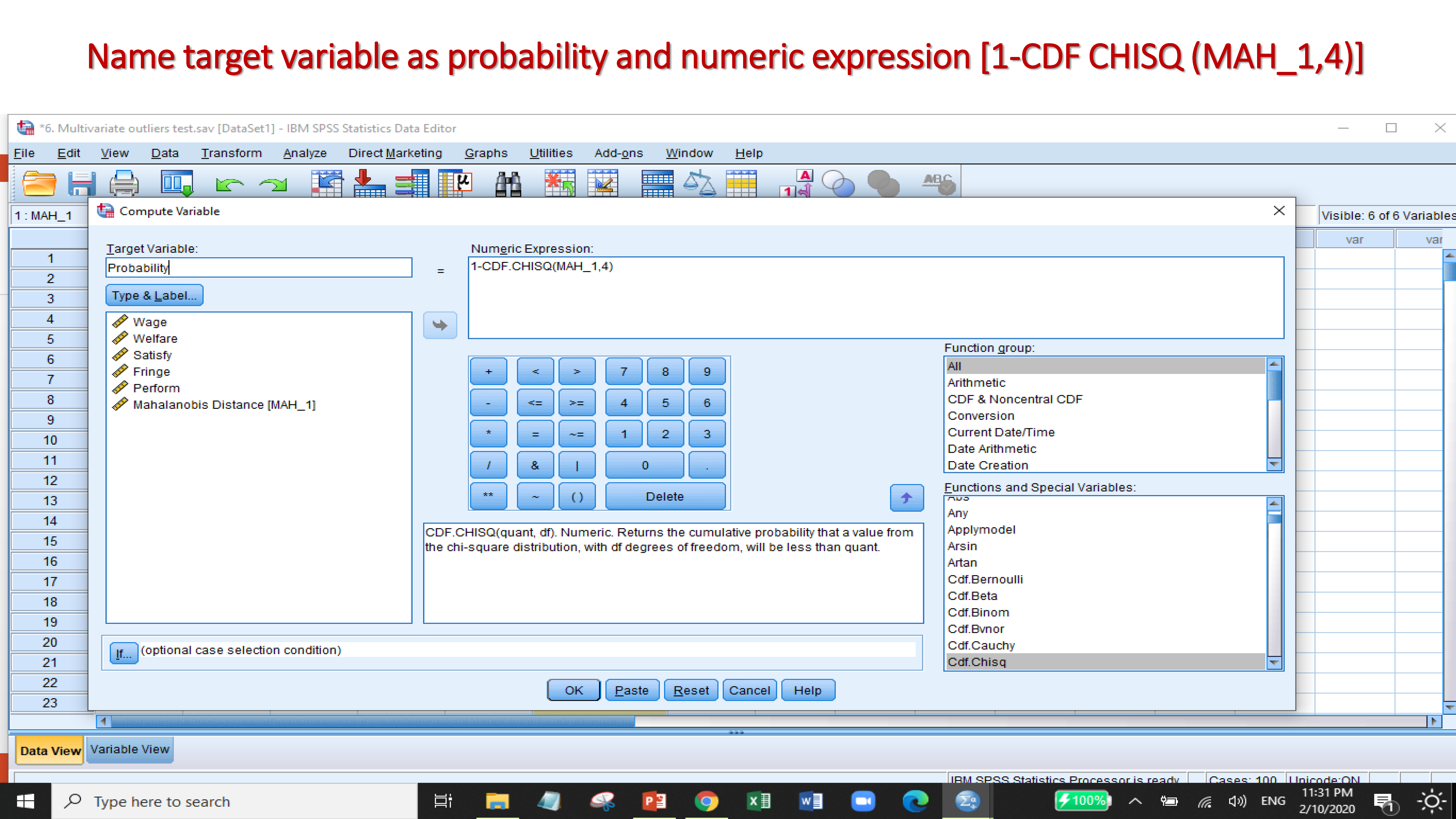
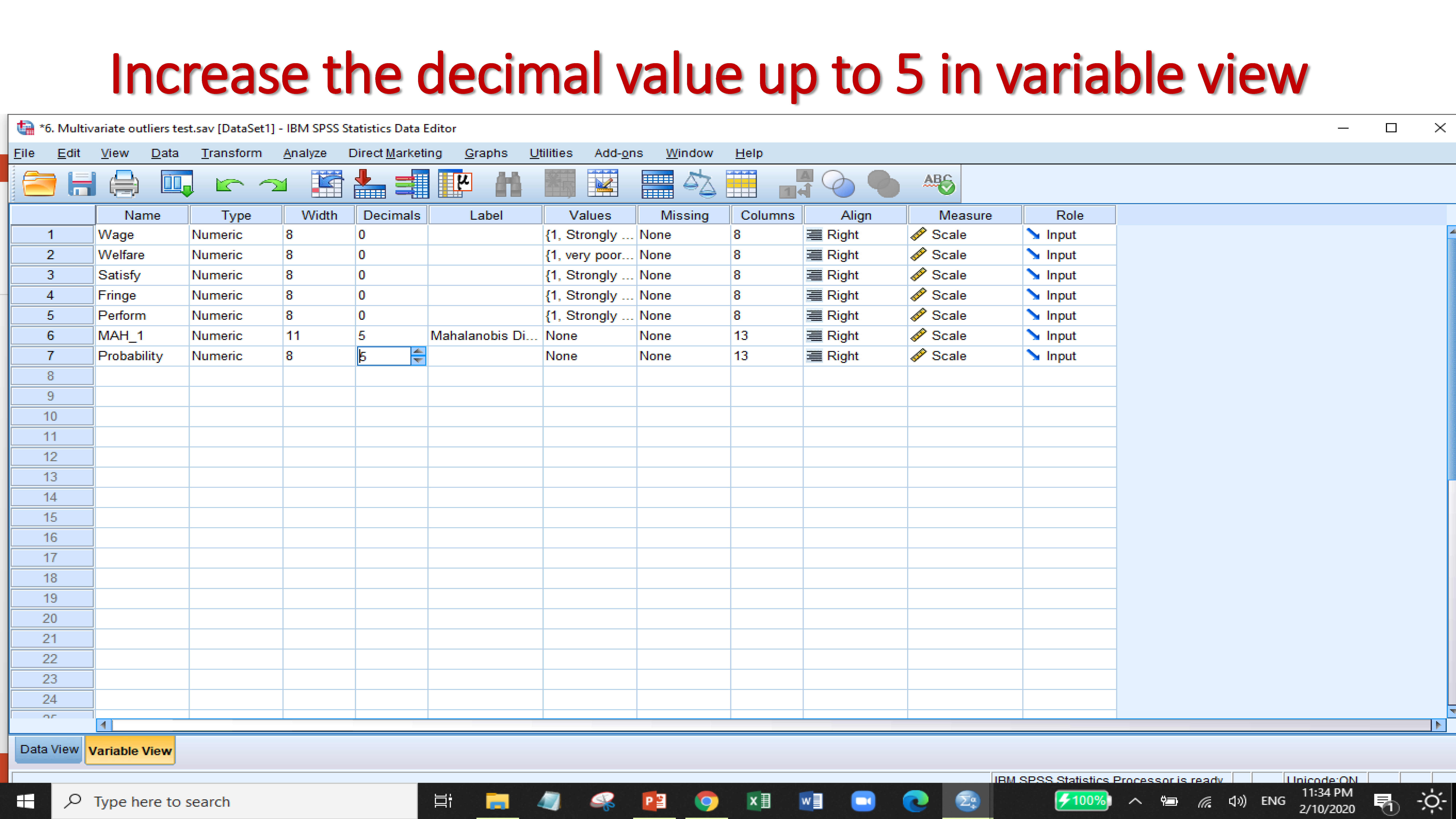
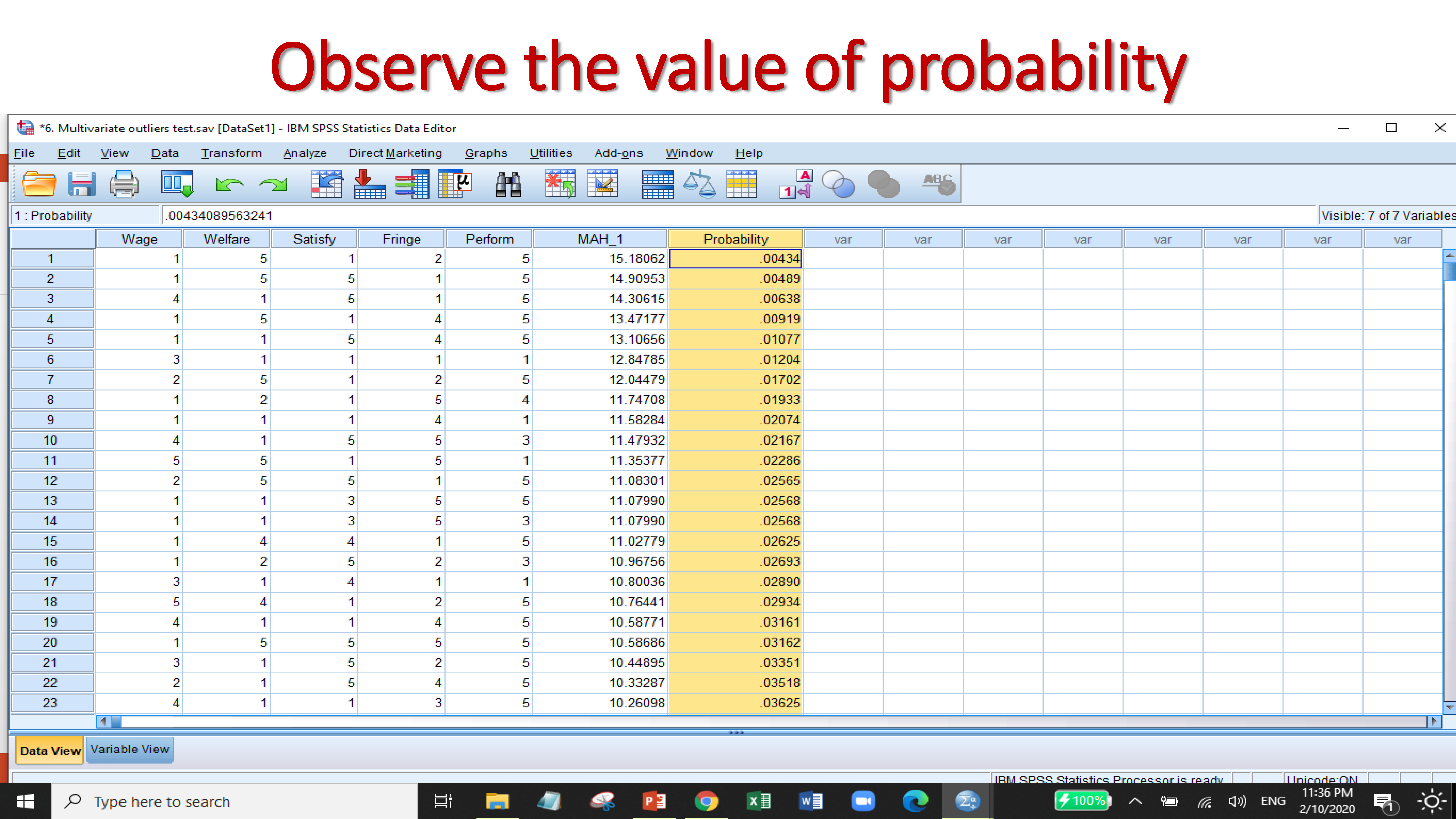
If the value of probability less than 0.001 then the observations will count as multivariate outliers.